Quantum computing works on several key phenomena in quantum mechanics, including superposition, entanglement, and interference.

Quantum mechanics

The quantum world is a fascinating and mysterious place that defies our everyday intuition. Unlike the classical world we are familiar with, where objects exist in well-defined positions and have precise properties, the quantum world is characterized by superposition, entanglement, and uncertainty.

At the heart of the quantum world is the concept of the quantum state, which describes the properties of a quantum system such as an atom or a particle. Unlike classical systems, where the state of an object can be fully described by a set of well-defined properties, the quantum state is described by a wave function that encodes the probability distribution of the properties of the system.

One of the most striking features of the quantum world is superposition, which allows a quantum object to exist in multiple states at the same time. For example, an electron can exist in a superposition of two energy levels simultaneously, or a photon can exist in a superposition of two polarizations at the same time.

Another important feature of the quantum world is entanglement, which occurs when two quantum systems become correlated in a way that is not possible in the classical world. Entanglement allows quantum systems to share information in a way that is faster than the speed of light and is the basis for many applications in quantum computing and quantum communication.

While the quantum world may seem strange and unfamiliar, it has enormous potential to revolutionize fields such as computing, cryptography, and material science. As we continue to explore the quantum world, we are discovering new and exciting ways to harness its unique properties for practical applications.

"Reality is merely an illusion, albeit a very persistent one." - Albert Einstein

Quantum Superposition

In traditional Digital computers, the information is stored in the form of Bits. which can only have two possible values (0 or 1), but in Quantum Computers we use qubits. Qubits are the basic building blocks of quantum computers. qubits can have a superposition of both 0 and 1 at the same time. This means that qubits can represent more information than classical bits. and that makes the quantum computer more powerful

let's simply understand this qubits phenomenon by taking the example of coin flipping

Let's say you have a bunch of coins and you want to determine how many of them are heads and how many are tails. With a traditional computer, you would have to flip each coin one by one and count the number of heads and tails. This can be a slow and time-consuming process, especially if you have a large number of coins.

However, with a quantum computer, you can use a quantum algorithm called Grover's algorithm to search through all the coins and quickly find the ones that are heads or tails. This algorithm uses the concept of quantum superposition and entanglement to test multiple coins simultaneously and quickly find the ones that meet your criteria.

For example, let's say you have 8 coins and you want to find the ones that are heads. With a traditional computer, you would have to flip each coin one by one and count the number of heads. However, with a quantum computer using Grover's algorithm, you can test all the possible combinations of coins simultaneously and find the ones that are heads much faster.

This is just one example of how quantum computers can be used to solve problems faster than traditional computers. Quantum computers excel at problems that involve searching through a large number of possibilities or finding patterns in large amounts of data, while traditional computers are better suited for tasks that require precise and predictable calculations.

Quantum Tunneling

Quantum tunneling is a crucial aspect of quantum computing that enables the manipulation of qubits by allowing them to tunnel through potential barriers. One real-world example of this is the tunnel junction in a superconducting qubit.

A superconducting qubit is a type of qubit that uses superconducting materials to take advantage of quantum properties. In a superconducting qubit, a small piece of superconducting material is formed into a loop, called a Josephson junction. When a voltage is applied to the junction, it creates a potential barrier that separates two superconducting regions.

This potential barrier is analogous to a physical barrier that a particle would not be able to pass through according to classical mechanics. However, in the quantum world, the qubit can exist in a state of superposition, in which it partially exists on either side of the barrier and partially inside the barrier. If the barrier is thin enough and the qubit's energy is low enough, there is a probability that the qubit will tunnel through the barrier and interact with the qubit on the other side.

This tunneling can be used to perform quantum logic operations, such as the CNOT gate, which is a fundamental operation in quantum computing. The CNOT gate allows for two qubits to become entangled, which is an important property for quantum computing algorithms.

In summary, the tunnel junction in a superconducting qubit is an example of how quantum tunneling can be used in quantum computing to manipulate qubits. By creating a potential barrier, the qubits can tunnel through and interact with each other, enabling quantum logic operations that are essential for quantum computing algorithms.

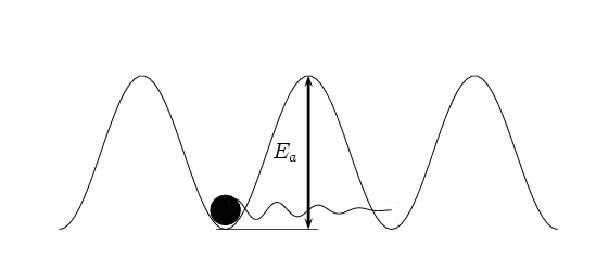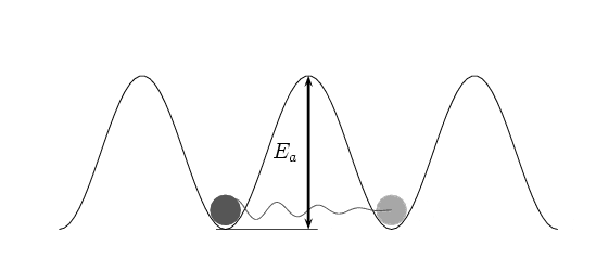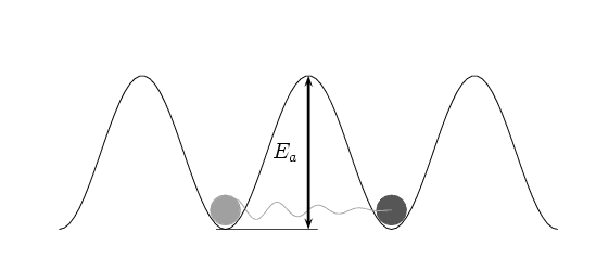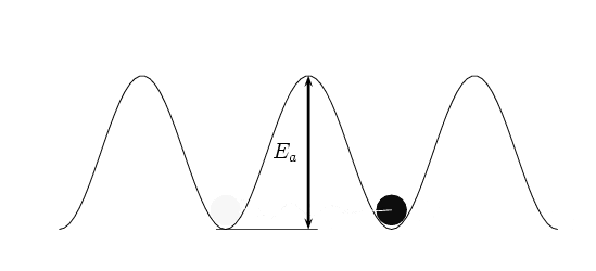
Entanglement

Entanglement is a strange phenomenon in the world of quantum mechanics that can occur regardless of the distance between two particles. This means that two entangled particles can be separated by vast distances, such as one on Earth and one in space.

To understand this, let's consider an example. Imagine we have two particles that are entangled, one on Earth and one in space. When we measure the state of the particle on Earth, the state of the particle in space is instantly determined, even if they are separated by millions of miles.

This may seem like magic, but it's a real phenomenon that has been observed in many experiments. Entanglement is not limited by distance and can occur across any distance, as long as the entangled particles remain isolated from their environment.

However, maintaining entanglement over long distances can be difficult, as the entangled particles are susceptible to noise and interference from their surroundings. This is why scientists are constantly working to develop new technologies and techniques to preserve entanglement and explore its potential applications, including quantum communication and cryptography.

Interference

Interference is a key concept in quantum computing that arises from the wave-like nature of quantum particles. In quantum mechanics, particles can exist in a state of superposition, meaning they can exist in multiple states simultaneously. When these superposition states combine, they can interfere with each other, leading to some interesting and counterintuitive effects.

To understand interference in quantum computing, consider an example of a particle that can exist in two states, "up" or "down," at the same time. If we were to measure this particle, we would collapse its superposition state into one of these two states. However, if we were to interfere with the particle's superposition state before measuring it, we could manipulate the probabilities of it being in the "up" or "down" state.

For instance, imagine we have two superposition states, one that is more likely to be in the "up" state and one that is more likely to be in the "down" state. If we interfere these two states in such a way that the "up" states reinforce each other and the "down" states cancel each other out, we could end up with a particle that is more likely to be in the "up" state when we measure it.

Interference can be used to perform quantum operations, such as creating entangled states, performing quantum algorithms, and correcting errors in quantum systems. However, interference can also be a source of noise and error in quantum systems, as it can be disrupted by environmental factors and other sources of interference.

Imagine we have a quantum computer with two qubits, labeled qubit A and qubit B. Each qubit can be in a superposition of two states, 0 and 1, at the same time. The superposition state of the two-qubit system can be represented as a linear combination of all possible two-bit strings, like this:

|Ψ⟩ = α|00⟩ + β|01⟩ + γ|10⟩ + δ|11⟩

Here, α, β, γ, and δ are complex numbers that represent the probability amplitudes of each state.

Now, suppose we apply a quantum gate to qubit A that flips its state if qubit B is in the state 1. This is called a Controlled-NOT (CNOT) gate. The effect of this gate is to create an interference pattern in the superposition state.

Specifically, if qubit B is in the state 1, the CNOT gate will flip the state of qubit A. This will create a negative sign in front of the state |11⟩ in the superposition, which will interfere with the other states. The resulting superposition state will look like this:

|Ψ⟩ = α|00⟩ + β|01⟩ + γ|10⟩ - δ|11⟩

Notice that the state |11⟩ has a negative sign, which means it will interfere destructively with the other states. This interference pattern can be used to perform various operations in quantum computing, such as creating entangled states and implementing quantum algorithms.

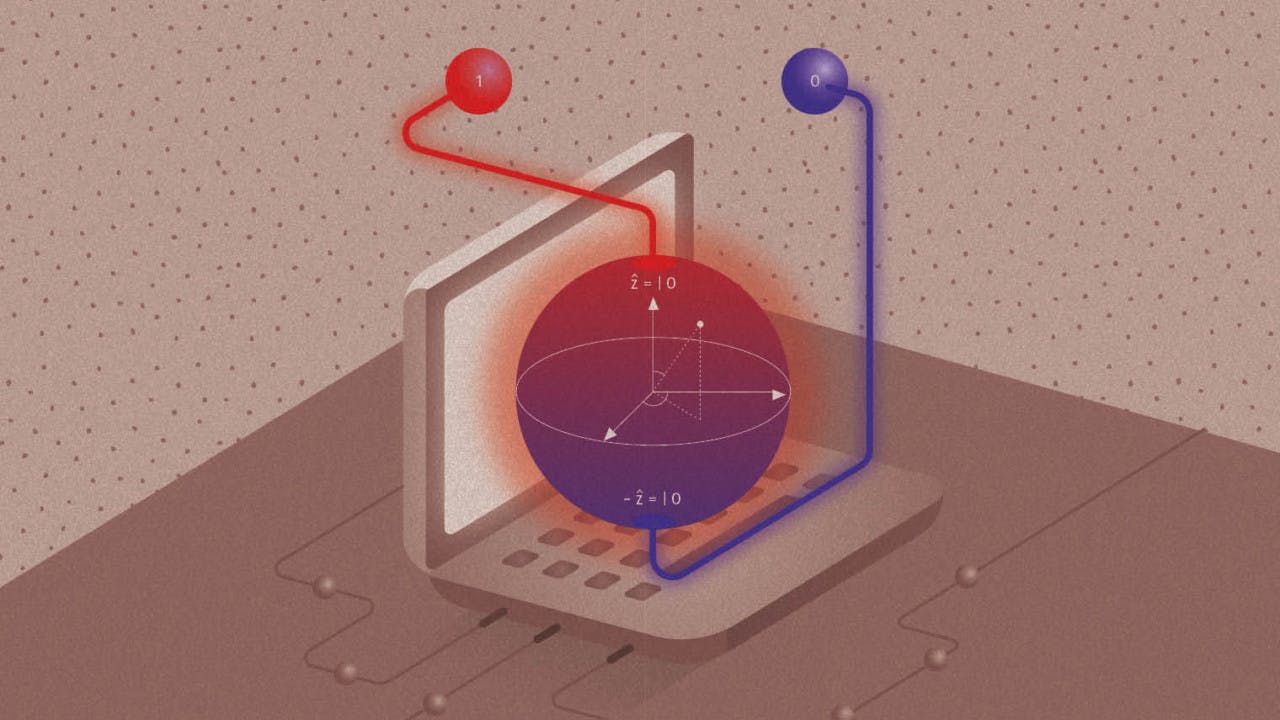
In conclusion, let me leave you with a quote from renowned physicist Richard Feynman: "Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy." Quantum computing is indeed a wonderful problem, but it is one that we are steadily making progress on, and the potential rewards are enormous. As we continue to explore the quantum world and push the boundaries of what is possible, we may well unlock new insights and capabilities that we cannot even imagine today.